跳至正文
首页 » 数字滤波器设计

数字滤波器设计

滤波器最早是由电容电阻组成的频率选择电路，可以提取需要的频段，去除无用信息。在程序设计时也将实现类似功能的程序成为滤波器。如果用自动控制理论的方式考虑，任何系统都是对输入信号不同频段的缩放和相移。广义的讲任何系统都可以成为一个滤波器，只不过很难直接（或者说很难总结出系统的方法）将系统特性修改成我们需要的样子，所以才选择使用电子器件或者程序来设计滤波器。本文将简要地介绍 数字滤波器设计 的基础。

仍然以两轮车为例，现在需要解决的问题其在某个频率的共振问题。像前面所说，可以通过修改车体（如增加配重、改变质量分布等）改变其固有频率来解决，但是如何修改就要经过复杂的计算，而且很多控制对象是不允许进行修改的。这时我们在传感器侧、电机侧添加一个滤波电路，或者在控制器中设计一个数字滤波器都可以很便捷的解决这个问题。

1 离散数字滤波器的实现

考虑一个比较通用的线性时不变系统——常系数线性差分方程

y(n) = -\sum^N_{k=1} a_ky(n-k)+\sum^M_{k=0}b_kx(n-k) \tag{1.1}

当 a_k 不全为零且 N \geqslant 1 时，当前时刻系统输出与前 N 个时刻系统输出相关。而之前时刻的系统输出又与该时刻前N个时刻的系统输出相关。如此递推可以得知当前系统输出与之前所有的系统输出相关。当以这样的系统作为滤波器的时候称其为无限长脉冲响应滤波器（IIR 滤波器、infinite impulse response filter）。

当 a_k 全为零时，方程 （1.1）可以简化为

y(n) = \sum^M_{k=0}b_kx(n-k) \tag{1.2}

当前时刻的系统输出仅与前 M 个时刻的系统输入相关，而每个时刻的系统输入都是独立的。因此当前时刻的系统输出仅与前 M 个时刻的系统相关。当以这样的系统作为滤波器的时候称其为有限长脉冲响应滤波器（FIR 滤波器、finite impulse response filter）。

IIR 滤波器在实际应用时有线性相位问题，一般在参数数量相同的情况下，在阻带中的旁瓣更低。所以在实时性要求较高的地方使用 FIR 滤波器，而在实时性要求较低的场合使用 IIR滤波器。

2 FIR 滤波器设计

2.1 对称的 FIR 滤波器

可以将式 （1.2） 整理成系统单位冲击响应与输入信号的卷积形式。

y(n)=\sum^M_{k=0}h(k)x(n-k)=(h*x)(n)

进行 Z 变换得到 Y(z)=H(z)X(z)

可以看到H(z)完整描述了系统，称其为系统函数。系统函数对不同频段的作用即可标志滤波器对输入信号的作用。

系统的单位脉冲响应对称时h(n)=h(M-1-n)\quad n=0,1,\ldots ,M-1

由定义得 \begin{aligned}H(z)&=h(0)+h(1)z^{-1}+ \cdots +h(M-1)z^{-(M-1)} \\&=z^{-(M-1)/2}\{h(\frac{M-1}{2} )+\sum^{(M-3)/2} _{n=0} h(n) [z^{(M-1-2n)/2}+z^{-(M-1-2n)/2}] \}\quad M为奇数\\ &=z^{(M-1)/2} \sum^{(M/2)-1}_{n=0}h(n)[z^{(M-1-2n)/2}+z^{-(M-1-2n)/2}] \quad M为偶数 \end{aligned}

利用欧拉公式（e^{j\omega}=\cos\omega+j\sin\omega）变换到频域中进行分析H(\omega)=H_r(\omega)e^{-j\omega(M-1)/2}

其中H_r是一个实函数，可以表示为 \begin{aligned}H_r(\omega)&=h(\frac{M-1}{2})+2\sum^{(M-3)/2}_{n-0}h(n)\cos\omega(\frac{M-1}{2}-n) \quad M为奇数 \\&=2\sum^{(M-1)/2}_{n-0}h(n)\cos\omega(\frac{M-1}{2}-n) \quad M为偶数\end{aligned}

相位特征可以表示为\theta(\omega)=\begin{cases}-\omega(M-1)/2 \quad H_r(\omega)>0 \\-\omega(M-1)/2+\pi \quad H_r(\omega)<0 \end{cases}

2.2 使用窗函数设计线性相位 FIR 滤波器

上节中是在已知系数对称时，分析 FIR 滤波器的效果。而更多情况是先根据实际需求得到滤波器的频率响应，再设计滤波器参数去逼近该响应。

已知频率响应 H_d(\omega) ，进行傅里叶逆变换得到相应的单位冲击响应 h_d(\omega) H_d(w)=\sum^\infty_{n=0}h_d(n)e^{-j\omega n}\quad h_d(n)=\frac{1}{n} \int^\pi_{-\pi}H_d(\omega)e^{j\omega n}\mathrm{d}\omega

从上式中可以看到从 h_d 到 H_d 经过了零到无穷的求和，而这在实际应用中是无法实现的。若设计一个长度为 M 的滤波器，则只能在 0 到 M-1 进行求和。相当于在原求和式上加了一个窗口，忽略窗口以外的数据。

定义矩形窗：\omega(n)=\begin{cases} 1,\quad n=0,1,\ldots,M-1 \\ 0,\quad \mathrm{others}\end{cases}

那么实际滤波器的单位脉冲响应变为h(n)=\omega(n) h_d(n)

矩形窗的傅里叶变换为\begin{aligned}W(\omega)&=\sum^{M-1}_{n=0}e^{-j\omega n} \\ &=\frac{1-e^{-j\omega M}}{1-e^{-j\omega}} =e^{-j\omega (M-1)/2}\frac{\sin(\omega M/2)}{\sin(\omega/2)}\end{aligned}

数字滤波器设计 _ 矩阵窗频率响应
图3.1 矩形窗频率响应

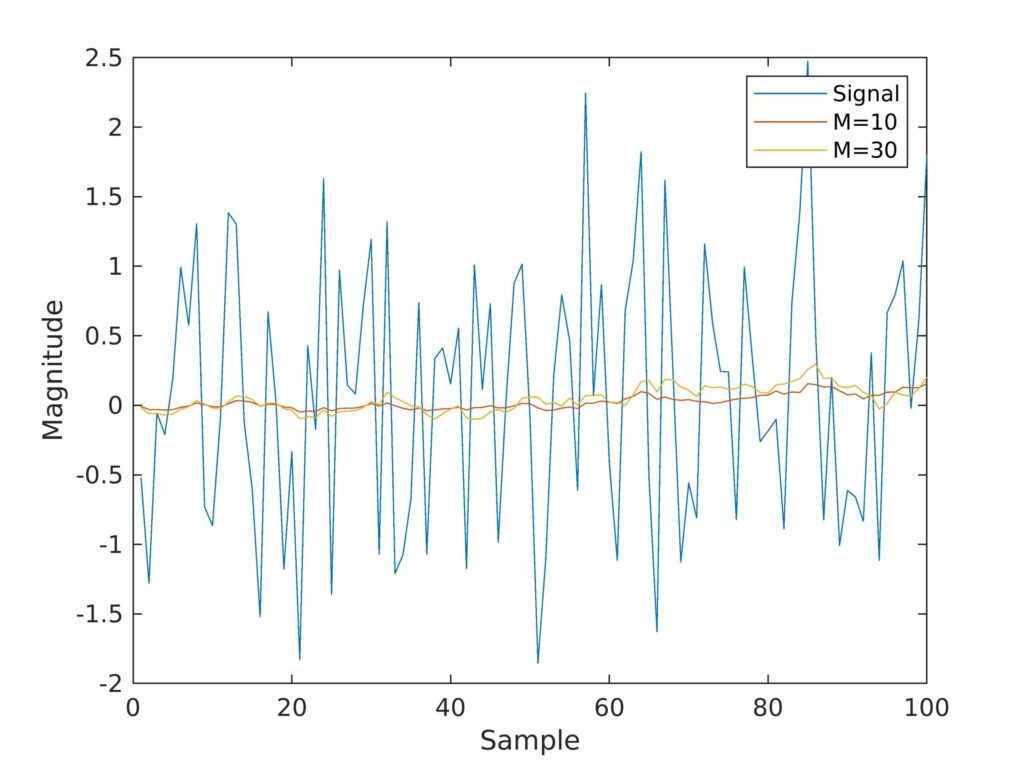
直接看矩形窗的频率响应不是很直观，下面将矩形窗加到平均滤波器上，并对一个随机信号进行滤波处理

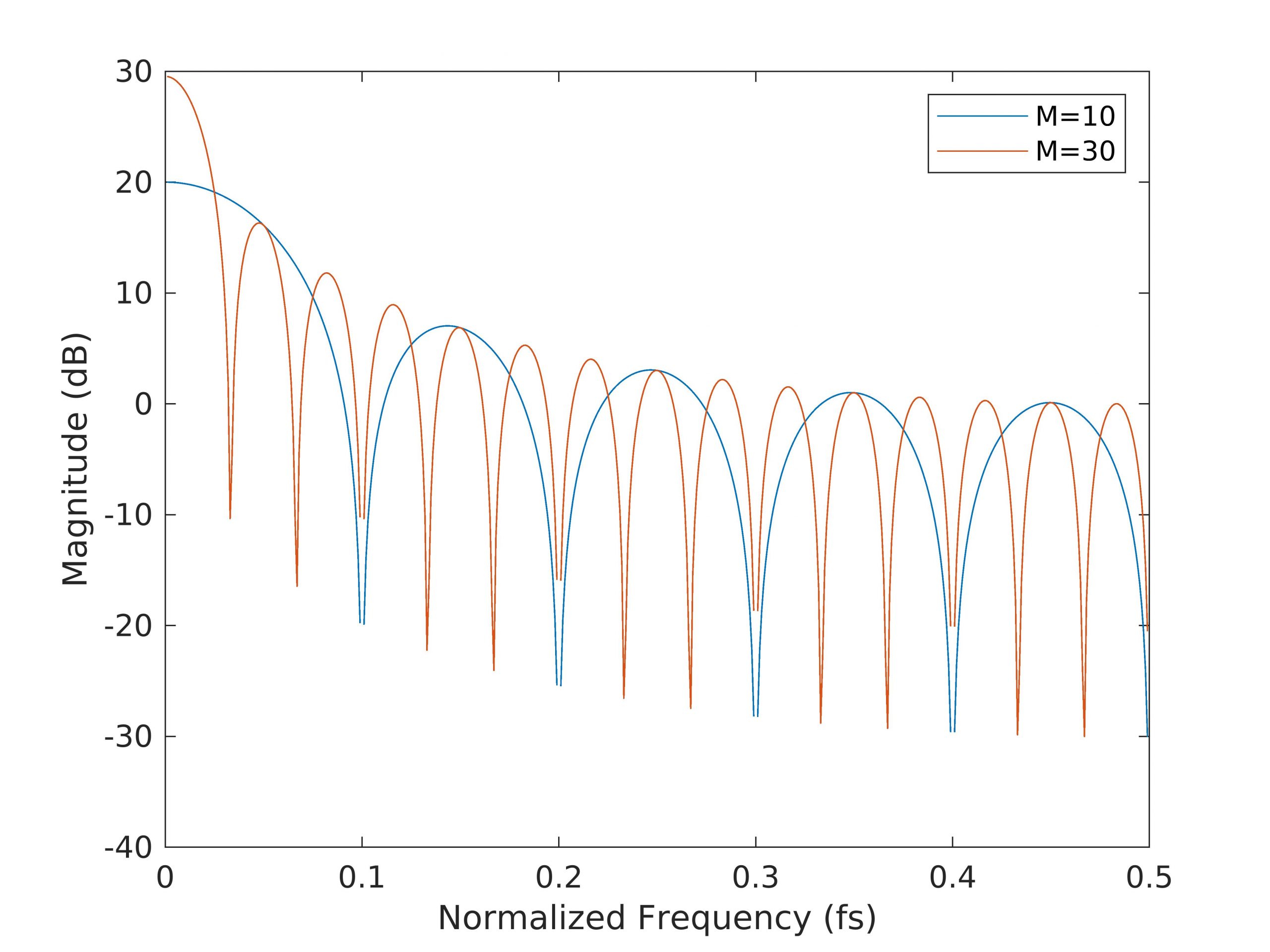
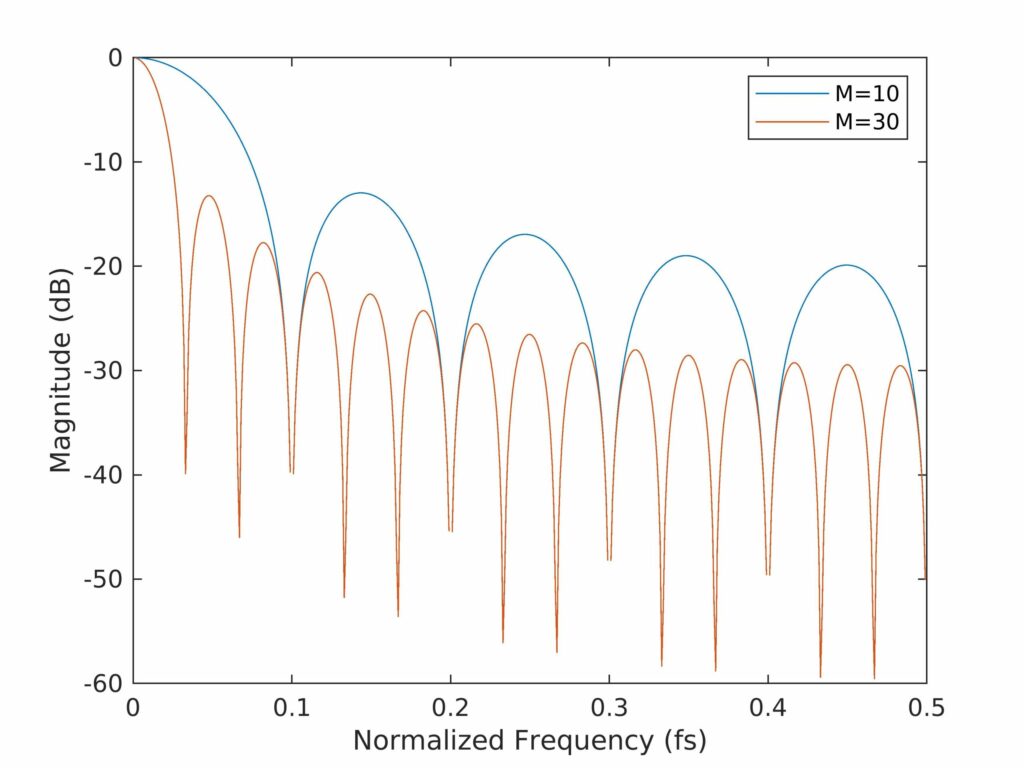
数字滤波器设计 _ 平均滤波器矩阵窗频率响应
图3.2 归一化后的矩形窗频率响应
数字滤波器设计 _ 平均滤波器矩阵窗滤波结果
图3.3 正态分布随机数的滤波效果
数字滤波器设计 _ 窗函数对正弦函数的影响
图3.4 窗函数对正弦函数的影响

如 图3.3 所示，窗函数本身会起到平滑作用，而这种平滑作用会随着主瓣宽度的变窄而变小。这由于随着 M 的增加，主瓣宽度会变窄，如 图3.2 所示。

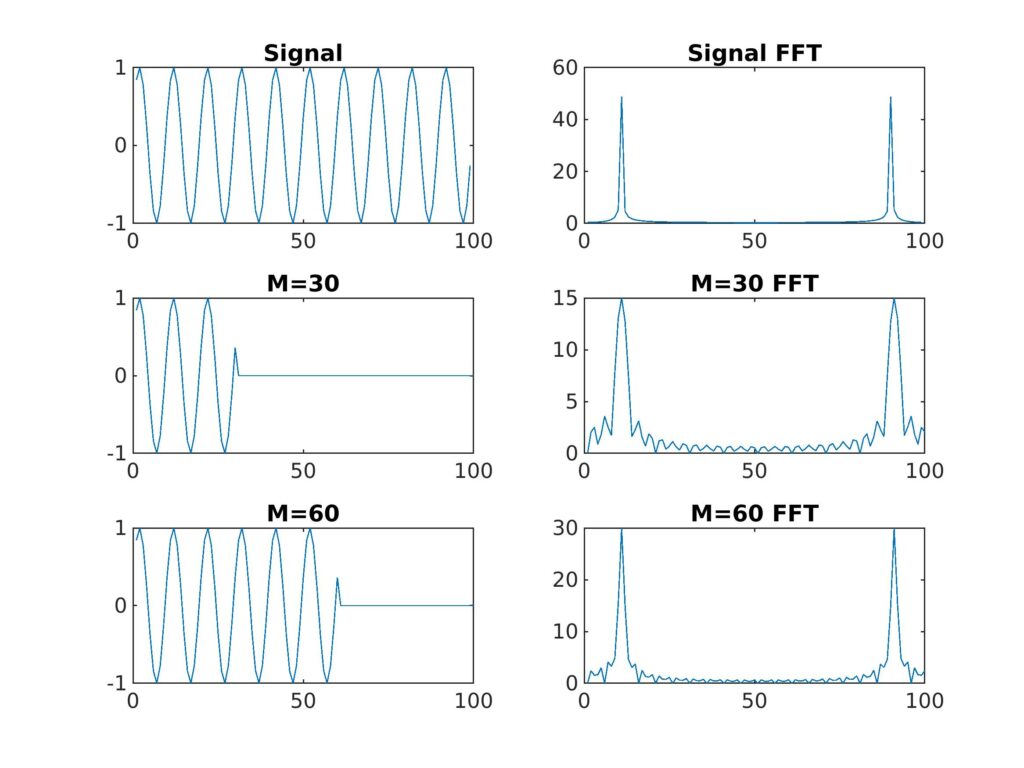
如 图3.4 所示，如果是干净无限长的正弦信号，那么它的傅里叶变换结果应该是两条线（Signal 不是无限长，相当于 M=100，所以不是两条线）。随着 M 的减小，主瓣高度会变低，旁瓣高度变高，这称为功率谱泄露（Spectral leakage）。这对应着 图3.2 中的旁瓣高度， M 越大，旁瓣高度越低。

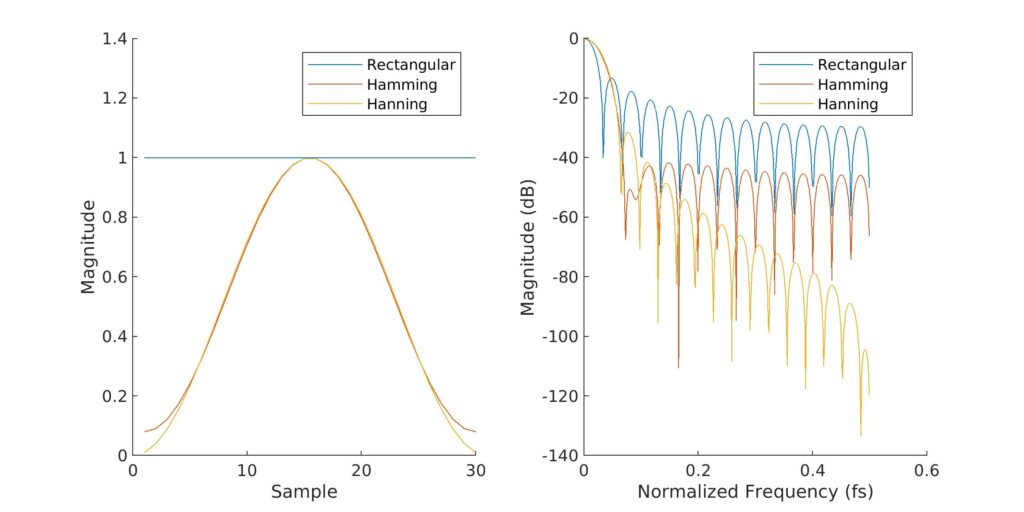
希望即保持平滑作用，又不想引入更多功率谱泄露。所以除了矩形窗，诞生了很多窗函数，以使主瓣宽度变宽，旁瓣高度变低。以 Hamming 和 Hanning 为例

Hamming：0.54-0.46\cos \frac{2\pi n}{M-1}
Hanning：\frac{1}{2}(1-\cos \frac{1 \pi n}{M-1})

数字滤波器设计 _ Hamming & Hanning
图3.5 Hamming & Hanning

3 IIR 滤波器设计

因为模拟滤波器设计已经比较完善，所以 IIR 滤波器设计过程多为先根据滤波器的指标要求设计一个模拟滤波器，再将其离散化转换为 IIR 滤波器。模拟滤波器设计方法和离散化过程都有很多，这里以巴特沃斯滤波器和双线性变换为例进行说明。

3.1 巴特沃斯滤波器设计

巴特沃斯滤波器，也被称为最大平坦滤波器，最先由 Stephen Butterworth 于 1930 年提出。本文不对该滤波器的原理进行讨论，直接使用结论。

一个 n 阶巴特沃斯低通滤波器的增益 G(\omega) 表示为
G^2(\omega)=\mid H(j \omega)\mid ^2 = \frac{G_0^2}{1+(\frac{\omega}{\omega_c})^{2n}} \tag{3.1}
其中， n 为滤波器阶数， \omega_c 为截止频率（功率下井为 -3 分贝时的频率）， G_0 是直流增益。

3.1.1 计算阶数

根据指标要求，在指定的频率 \omega_s ，满足衰减 \delta ，计算滤波器所需要的阶次。

将指定的频率 \omega_s 带入式 （3.1） 得 \delta^2 = \frac{G_0^2}{1+(\frac{\omega_s}{\omega_c})^{2n}}

解得 n=\frac{\lg(\frac{G_0^2}{\delta^2}-1)}{2\lg (\frac{\omega_s}{\omega_c})}

3.1.2 计算极点

通过拉普拉斯变换得到 H(s)H(-s)=\frac{G_0^2}{1+(\frac{-s^2}{\omega_c^2})^n}
H(s)H(-s) 的极点均匀地分布在半径为 \Omega_c 的圆上： \frac{-s^2}{\Omega_c^2}=(-1)^{1/n}=e^{j(2k+1)\pi /n}, \quad k=0,1,\ldots, N-1
所以有 s_k=\Omega_c e^{j \pi /2}e^{j (2k+1)\pi/2n}\tag{3.2}

3.2 双线性变换

前面已经设计了模拟滤波器，现在将其离散化。常见的离散化工具有导数逼近法，冲击不变法和双线性变换。以双线性变换为例是因为它使用的范围更广（另外两种方法仅适用于低通滤波器和一类有限的带通滤波器）。

考虑一个简单的系统函数 H(s)=\frac{b}{s+a}

转换成微分方程形式则是 \frac{\mathrm{d}y(t)}{\mathrm{d}t}=ay(t)+bx(t) \tag{3.3}

使用积分代替导数，并用梯形公式进行近似得 y(t)=\int_{t_0}^t y'(\tau)\mathrm{d}\tau+y(t_0)

考虑从时刻 (n-1)T 考虑时刻 nT 的系统输出 y(nT)=\frac{T}{2}[y'(nT)+y'(nT-T)]+y(nT-T) \tag{3.4}

同样将 nT 时刻带入式 （3.3） y'(nT)=-ay(nT)+bx(nT)

带入 式 （3.4）得， (1+\frac{aT}{2})y(n)-(1-\frac{aT}{2})y(n-1)=\frac{bT}{2}[x(n)+x(n-1)]

进行 z 变换 (1+\frac{aT}{2})Y(z)-(1-\frac{aT}{2})z^{-1}Y(z) =\frac{bT}{2}(1+z^{-1})X(z)

写成传递函数形式 H(z)=\frac{Y(z)}{X(z)}=\frac{b}{\frac{2}{T}(\frac{1-z^{-1}}{1+z^{-1}})+a}

参照原系统函数可以看到 s 平面和 z 平面得关系 s=\frac{2}{T} ( \frac{1-z^{-1}}{1+z^{-1}} )

将这个关系称为双线性变换。

4 参考文献

发表回复

您的邮箱地址不会被公开。 必填项已用 * 标注