常见流量计测量原理

本文将介绍几种常见地流量计测量原理，覆盖气体、液体等流体。根据工作原理不同可以分为差压式、热式、科里奥利力、超声式等。

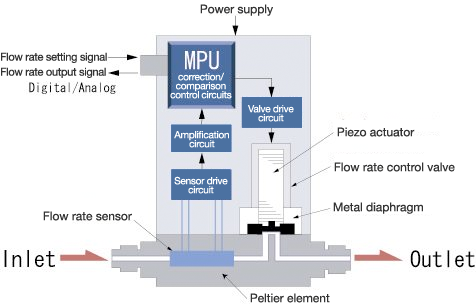
压差式质量流量控制器

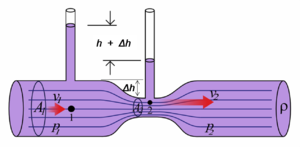
孔板式、文丘里喷嘴等差压式流量计，都以伯努利方程和流体连续性方程为依据。当流体经过阻流器件前后会产生压差，差值与流量的平方成正比。

原始表述：

\frac{1}{2}\rho v^2+\rho gh + p= 常数 \tag{1.1}

其中 $v$ 为流体速度， $g$ 为重力加速度， $h$ 为流体处于的深度， $p$ 为流体受到的压强， $\rho$ 为流体质量密度。

使用伯努利方程需要满足假设：

定常流动：流体性质不随时间变化
不可压缩：密度为常数，流体为气体时适用于马赫数小于0.3的情况
无摩擦：摩擦效应可以忽略
沿流线流动：流体元素沿流线流动，流线彼此不相交

对可压缩流体，可近似为

\frac{v^2}{2}+(\frac{\gamma}{\gamma-1})\frac{p}{\rho}=(\frac{\gamma}{\gamma-1})\frac{p_0}{\rho_0}\tag{1.2}

其中 $v$ 为流体速度， $\gamma$ 为绝热指数， $p_0$ 为总压力， $\rho_0$ 为总密度。

文丘里式

意大利物理学家文丘里发现，高速流动的气体附近压强减少。对于不可压缩流体（液体或低速气体），伯努利方程(1.1)可近似为：

p_1-p_2=\frac{\rho}{2}(v^2_2-v^2_1)

其中 $\rho$ 是流体密度， $p$ 是压力， $\rho$ 是流体密度。

孔板式

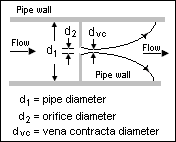
孔板式流量计在流道中间有个带有孔洞的薄板，流体流过时两侧会产生压差。流体穿过孔洞后，流量会随之增加，压力降低。最终汇聚在缩口颈（图中 vena contracta）达到流量最大值、压力最小值，之后又逐渐散开，流量减小，压力增大。

由伯努利方程加上经验公式得

q_m=\frac{C_d}{\sqrt{1-\beta^4}}\epsilon\frac{\pi}{4}d^2\sqrt{2\phi_1\Delta p}

其中 $q_m$ 是质量流量，单位为kg/s； $C_d$ 是流出系数（coefficient of discharge），没有量纲，与孔洞的几何尺寸和接头相关，通常在0.6~0.85之间； $\beta$ 是孔洞直径 $D$ 和管路内径 $D$ 之间的比率； $\epsilon$ 是流体的膨胀系数，1表示不可压缩流体； $\rho_1$ 孔洞前的流体密度； $\delta p$ 孔洞前后压差

层流式

气体在流道中流速不均匀，影响流量计测量精度和稳定性。该现象可用雷诺数（Re）来量化：

R_e=\frac{\rho uD_H}{\mu}

其中， $\rho$ 是流体密度 $D_H$ 是流道直径，u 是流道内平均流速， $\mu$ 是动力粘度。

工程应用中通常取小于2000为层流，大于4000为湍流，中间为过度状态。

层流式流量计的流道由许多流道片叠加而成，每层流道的等效 $D_H$ 很小，以此获取更小的雷诺数，使气体在其中以层流状态。

在层流状态下，粘滞力为主要影响因素。以一段毛细管为例，讨论流量和压差之间关系，可使用泊肃叶定律描述：

\Delta P=\frac{8\mu L Q}{\pi r^4}

其中 $\Delta P$ 是压力损失， $L$ 是毛细管长度， $\mu$ 是粘度系数， $Q$ 是体积流量， $r$ 是毛细管的半径。

可以看出虽然层流式和孔板式都是差压原理，但是依托的原理不同。层流差压式线性度更好，同时流道中流体流动更稳定。

热式质量流量控制器

热式质量流量控制器是利用流体流过外热源加热的管道时产生的温度场变化，或加热流体时流体温度上升到某一值所需要的能量来测量流体质量流量。

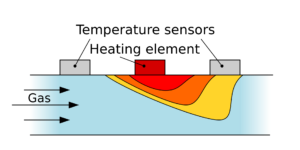
直插式（inline sensor）

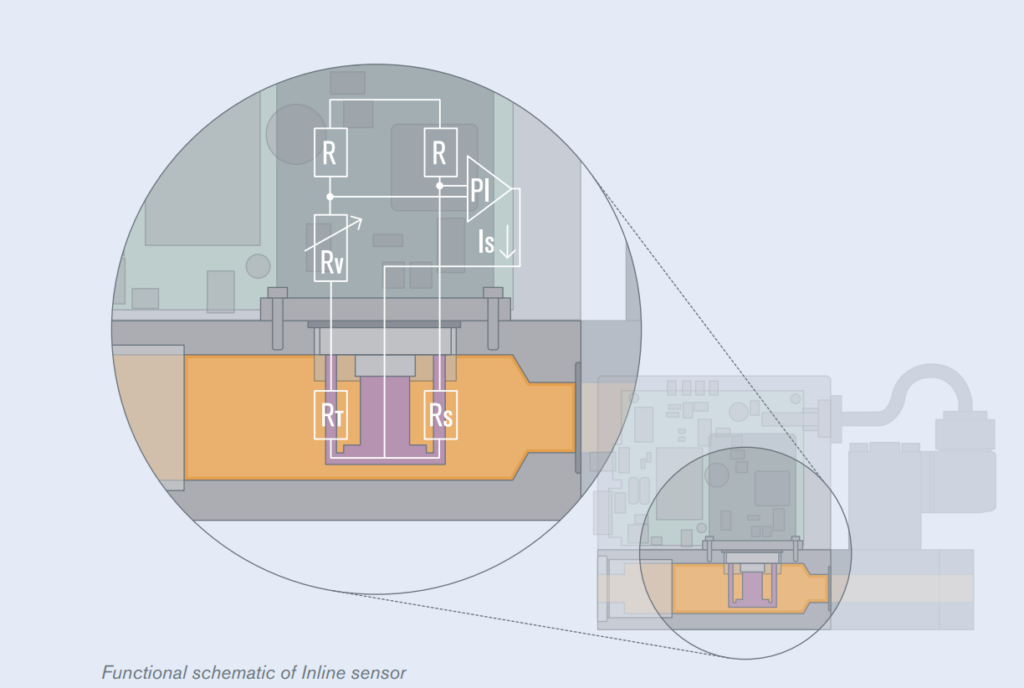
直插式流量计测量单元直接置于主流道中，由加热电阻 R_s 和测量电阻 R_T 组成，工作在 CTA（ Constant Temperature Anemometer）模式。

微电子机械式（MEMS sensor）

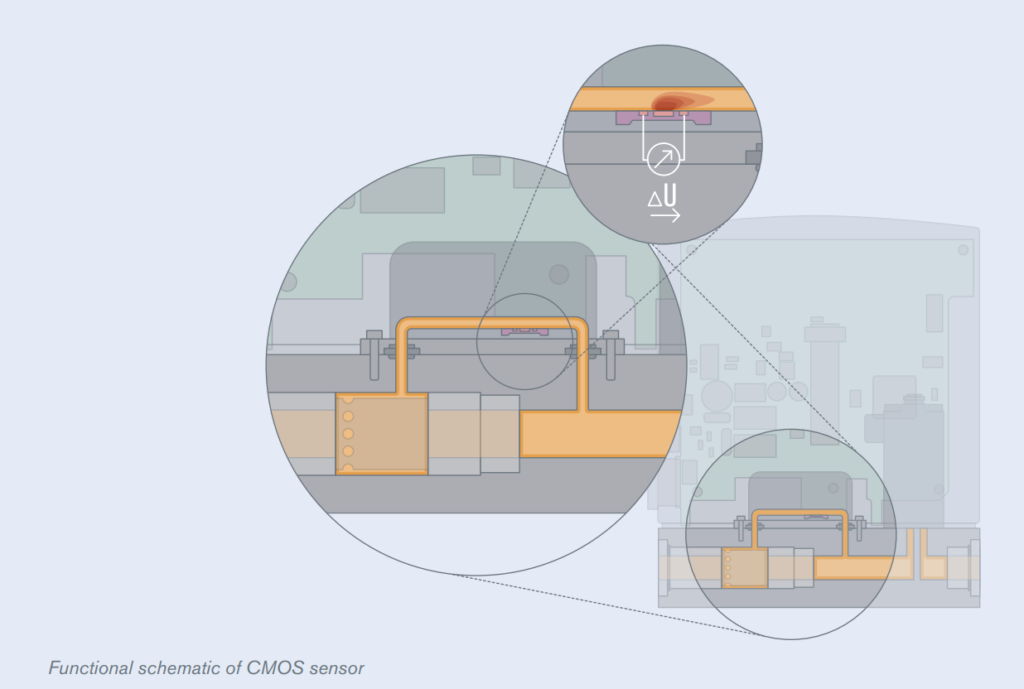
与插入式直接测量主流道不同，通常 MEMS 式测量分流后的支路。为保持主流道和支路的分流比，主流道中安装有整流器件，而这种方式也会增大压损。

毛细管式（Capillary sensor）

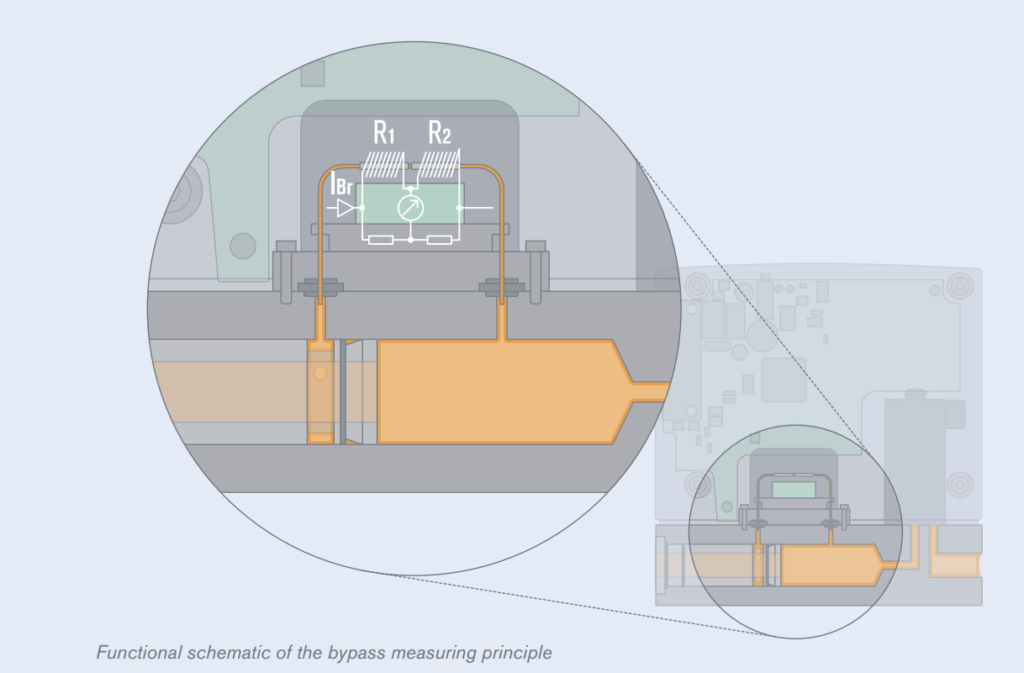
毛细管式同 MEMS 式一样，主流道需要整流器件，测量单元位于支路上。电阻丝绕在毛细管上，不直接与气体接触，可以增强耐腐蚀性，降低漏率。

科里奥利流量计（Coriolis）

科里奥利力是一种惯性力，是对旋转体系中进行运动的质点由于惯性相对于旋转体系产生偏移的现象的表述。

\vec{F_c}=-2m(\vec{\omega}\times\vec{v})

其中 $\vec{F_c}$ 为科里奥利力， $m$ 为质点质量， $\vec{\omega}$ 为旋转体系的角速度， $\vec{v}$ 为质点的运动速度。

下图是科里奥利力流量计的结构示意图，其中 Vibration 为振动激励，Pickup sensor 为测量单元。

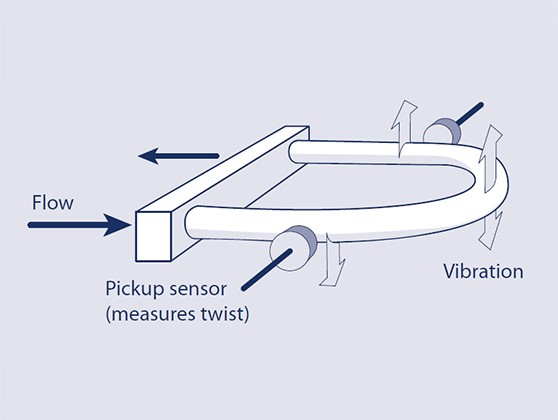
现取一时刻，振动激励顶部以 $v_p$ 的线速度运动，流道内流体以 $v_f$ 流动。

通过 $\omega=v/r$ 可以得到流道振动在这一时刻的角速度。

在两侧测量单元处，流道内流体流动方向相反，流道振动导致的角速度相同，带入科式力计算式得此时两位置收到的科式力大小相同，方向相反。

假定流体流动速度不变，科式力随角速度不断变化，不严谨地认为其展现出阻尼效果，影响振动相位。且由于两个检测位置的科式力方向相反，相位的影响也是相反的。所以利用该相位差可以测量流动速度。

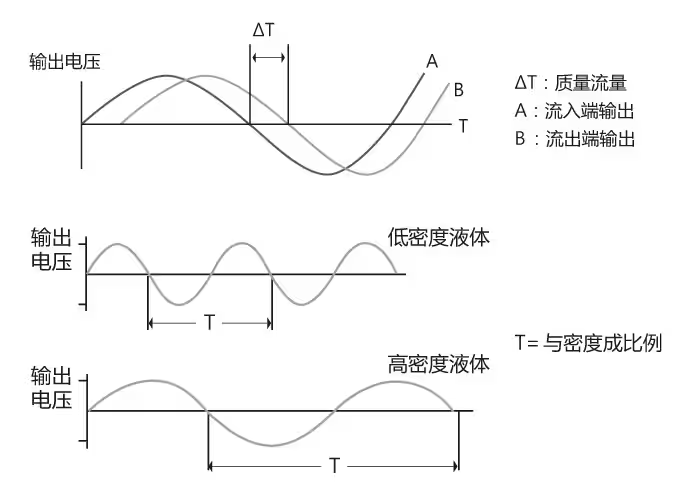
当流道中流过不同密度的流体，固有频率不同，可以通过该性质测量流体密度。

超声波流量计

时差法

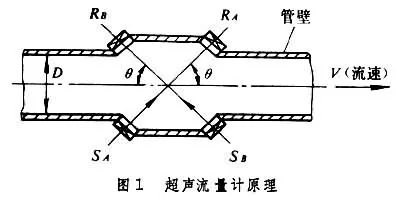
超声波通过流体时，传播速度会受流体的流动影响。

c\pm v \cos\theta = \frac{L}{t}

其中 $c$ 是流体内声速， $v$ 是流体流动速度， $\theta$ 是测量角度， $L$ 是传输距离， $t$ 是传输时间。

取图中 $R_A$ 、 $S_A$ 这一对通路，向上传播顺流体流动记传播时间 $t_{up}$ ，向下传播逆流体流动记传播时间 $t_{down}$ 。可得流体流速

v=\frac{L}{2\cos \theta}\frac{t_{up}-t_{down}}{t_{up}t_{down}}

频差法

当流体内含有气泡、小颗粒或湍流时，超声波会产生散射，发送信号和接收信号之间会产生多普勒频移。

多普勒效应表述为

f=(\frac{c\pm v_r}{c\mp v_s})f_0

其中 $f$ 是观测到的频率， $c$ 是流体内声速， $v_r$ 是接收者相对于介质的速度， $v_s$ 是发送者相对于介质的速度， $f_0$ 是发送频率。

在流量计的应用中，发送、接收器是固定在流道上的，接收、发送相对于介质的速度等于流体流速 $v$ 。

f=\frac{c\pm v}{c\mp v}f_0

在流速远小于声速时，可近似为

\delta f=\frac{2v}{c}f_0

涡街流量计（Vortex flowmeter）

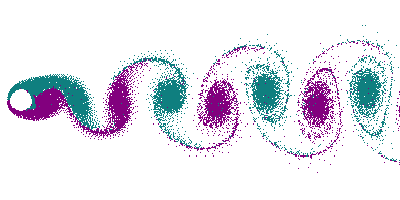
卡门涡街指在流体中安置阻流体，在特定条件下会出现不稳定的边界层分离，阻流体下游的两侧，会产生两道非对称地排列地漩涡。卡门涡街频率为：

f=\frac{St\times v}{d}

其中 $f$ 为卡门涡街频率， $St$ 为斯特劳哈尔数（~0.2）是一个描述周期性非定常流动地无量纲数， $v$ 为流体速度， $d$ 为阻流体迎面宽度。

常见流量计测量原理

压差式质量流量控制器

文丘里式

孔板式

层流式