本文介绍 拟凸函数 ( quasiconvex function ),包括其定义,Jensen 不等式、定义域为 R 基础性质,一阶、二阶条件的可微拟凸函数,可以保留拟凸性质的运算(权重非负的最大值、复合、最小值)。
1 定义
如果一个函数f:R^n\rightarrow R的定义域及其所有子集满足S_\alpha=\{x\in\mathrm{dom}f\mid f(x)\leqslant\alpha\}对任意\alpha \in R都是凸的,那么称函数f为拟凸函数(quasiconvex function)。也就是存在一个\alpha使函数值小于\alpha的部分是凸的,那么该函数为拟凸的。
类似的,当函数f满足S_\alpha=\{x\in\mathrm{dom}f\mid f(x)\geqslant\alpha\}都是凸的,那么称函数f为拟凹函数(quasiconcave function)。也就是如果-f是拟凸的,那么f是拟凹的。
若函数同时满足拟凸和拟凹,即满足S_\alpha=\{x\in\mathrm{dom}f\mid f(x)=\alpha\}那么称该函数为拟线性函数。
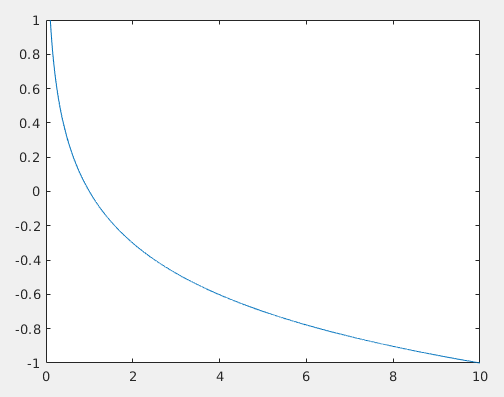
下面通过f(x)=log(x)作为例子
使用定义式进行说明,取\alpha=10得到S_{10}=[1,+\infty),是个凸集。类似的取其他\alpha,S_\alpha仍是一个凸集,所以f(x)=log(x)是个拟凸函数。取f(x)=-log(x)仍然可以得到类似的结论,所以f(x)=log(x)是一个拟凹函数。因为它既是一个拟凸函数也是一个拟凹函数,所以它是一个拟线性函数。
2 基础性质
2.1 Jensen不等式
拟凹凸性是之前讨论凹凸性的一种广义形式,所以仍可以保留很多凹凸性的性质或者拥有类似的性质。例如拟凸函数有Jensen不等式的变异形式:f(\theta x+(1-\theta)y)\leqslant max\{f(x),f(y)\}
2.2 定义域为R
拟凸函数的定义比较抽象,当定义为R时,可以用下面性质区别一个函数是否是拟凸函数。函数f:R\rightarrow R是拟凸函数当且仅当f至少满足以下一条性质
- f是不增的
- f是不减的
- 存在f定义域内一点c,使函数f在(-\infty,c)上不增,或在(c,+\infty)上不减
当定义第三条性质中的c为函数f的最小值点时,第三条性质则可以与前两条性质等价。
3 可微拟凸函数
3.1 一阶条件
若函数f:R^n\rightarrow R可微,那么函数f可微的充分必要条件是f的定义域是个凸集,并且对定义域内任意的x,y都有f(y)\leqslant f(x) \implies \nabla f(x)^T(y-x)\leqslant 0一阶条件下的可微拟凸函数的性质与凸函数的性质类似,但是有个区别:当\nabla f(x_c)=0时,若f(x_c)为最小值,但是拟凸函数的话则不一定。
3.2 二阶条件
设函数f:R^n\rightarrow R二阶可微,那么f是拟凸函数的充要条件是对x\in \mathbf{dom} f ,y \in R^n都有y^T\nabla f(x) \implies y^T\nabla^2f(x)y\geqslant0若定义域为R,那么条件则可以化简为f'(x)=0\implies f''(x)\geqslant 0也就是所有极值点都是极小值点。
4 可以保留拟凸性质的运算
4.1 权重非负的最大值
如果函数f_i,i=1,\ldots,n是拟凸的,权重\omega_i \geqslant 0, i=1,\ldots,n,那么他们的最大值函数f=max\{\omega_1f_1,\ldots,\omega_nf_n\}也是一个拟凸函数
4.2 复合
如果函数g:R^n\rightarrow R是拟凸函数,h:R\rightarrow R是不增的,那么复合函数f(x)=h(g(x))也是一个拟凸函数。
4.3 最小值
如果函数f(x,y)是拟凸函数,y的定义域C是一个凸集,那么函数g(x)=\mathop{inf}\limits_{y\in C}f(x,y)也是个拟凸函数