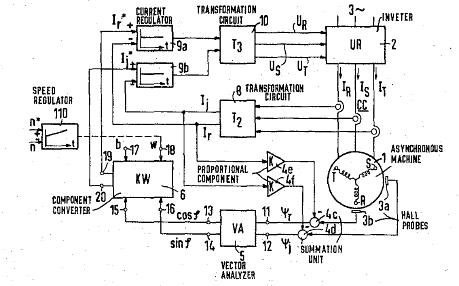
矢量控制(Vector Control, VC),也称为磁场导向控制(Field-Oriented Control, FOC),是通过Clarke变换和Park变换,将三相交流电变换为以一相为参考的三维垂直坐标系(dq0)。因为变换后的坐标系以一相为参考,所以三相交流电映射在三个轴上为直流量。
1 Clarke 变换
设三相电压为
\begin{cases} v_a = V_m \cos \omega t\\ v_b = V_m \cos(\omega t- 120^\circ) \\ v_c = V_m \cos(\omega t+ 120^\circ) \end{cases} \tag{1.1}Clarke 变换的目的是将其变换为
\begin{cases} v_\alpha = V_m \cos \omega t\\ v_\beta = V_m \sin \omega t \end{cases} \tag{1.2}将 (1.1) 用和角公式展开,再带入 (1.2) 得关系
\begin{cases} v_a = v_\alpha\\ v_b = - \dfrac{1}{2} v_\alpha + \dfrac{\sqrt{3}}{2} v_\beta\\ v_c = -\dfrac{1}{2} v_\alpha - \dfrac{\sqrt{3}}{2} v_\beta \end{cases} \tag{1.3}将对应关系写成矩阵形式即Clark 变换和Clark 反变换
\begin{bmatrix} v_\alpha \\v_\beta \end{bmatrix} = \dfrac{2}{3} \begin{bmatrix} 1 & -\dfrac{1}{2} & -\dfrac{1}{2} \\ 0 & \dfrac{\sqrt{3}}{2} & -\dfrac{\sqrt{3}}{2} \end{bmatrix} \begin{bmatrix} v_a\\ v_b\\ v_c \end{bmatrix} \begin{bmatrix} v_a \\ v_b \\ v_c \end{bmatrix} = \begin{bmatrix} 1 & 0\\ -\dfrac{1}{2} & \dfrac{\sqrt{3}}{2} \\ -\dfrac{1}{2} & -\dfrac{\sqrt{3}}{2} \end{bmatrix} \begin{bmatrix} v_\alpha \\ v_\beta\end{bmatrix}2 Park 变换
\alpha 、\beta 坐标系根据转子当前角度\theta旋转,可转换为直流量。旋转矩阵为
\begin{bmatrix} v_d \\ v_q \end{bmatrix} = \begin{bmatrix} \cos\theta & \sin\theta \\ -\sin\theta & \cos\theta \end{bmatrix} \begin{bmatrix} v_\alpha \\ v_\beta\end{bmatrix}在Clarke 变换上叠加旋转变换即Park变换
\begin{bmatrix} v_d\\ v_q\\ v_0 \end{bmatrix} = \frac{2}{3} \begin{bmatrix} \cos\theta & \cos(\theta - 120^\circ) & \cos(\theta + 120^\circ) \\ -\sin\theta & -\sin(\theta - 120^\circ) & -\sin(\theta + 120^\circ) \\ \frac{1}{2} & \frac{1}{2} & \frac{1}{2} \end{bmatrix} \begin{bmatrix} v_a\\ v_b\\ v_c \end{bmatrix}v_0是为了使变换阵可逆引入的变量,垂直于dq平面。
逆变换为
\begin{bmatrix} v_a\\ v_b\\ v_c \end{bmatrix} = \begin{bmatrix} \cos\theta & -\sin\theta & 1 \\ \cos(\theta - 120^\circ) & -\sin(\theta - 120^\circ) & 1 \\ \cos(\theta + 120^\circ) & -\sin(\theta + 120^\circ) & 1 \end{bmatrix} \begin{bmatrix} v_d\\ v_q\\ v_0 \end{bmatrix}3 电流环控制
电流的稳定对应电机输出转矩的稳定,在运动控制中起到了至关重要的作用。通过采样电阻得到电机三相上的电流后使用Park变换映射到dp0轴上。d轴(direct)为直接轴,相位与初相相同;q轴(quadrature)为正交轴,相位与初相相差90°;0轴理论上恒等于0。为使电机效率最高,控制目标为使d轴分量为0,通过改变q轴分量改变电机输出转矩。
因为电流环自身惯性小、带宽高、噪声大等特点,一般使用PI控制器(不使用D)。