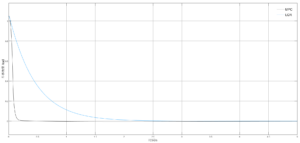
本文将对 LQR与MPC算法对比 ,并通过仿真结果说明MPC的优势。先使用LQR和MPC两种方法分别分析线性化后的两轮车模型,然后对比他们在处理时的区别,最后在仿真环境中对比两个算法设计的控制器处理线性化前非线性模型结果的仿真结果。
1 LQR
LQR (Linear-Quadratic Regulator) ,全称线性二次型调节器,可以根据系统模型设计一个最优状态反馈规律。
对于有限时间长度的离散时间线性系统(x_{k+1}=Ax_k+Bu_k),考虑性能指标:
J=x_N^TQx_N+\sum_{k=0}^{N-1} (x_k^TQx_k+u_k^TRu_k+2x_k^TNu_k)
使性能指标最小的控制规律为u_k=-K_kx_k
其中K_k=(R+B^TP_{k+1}B)^(-1)(B^TP_{k+1}A+N^T)
P_k由动态Riccati方程倒退时间迭代计算得
P_{k-1}=A^TP_KA-(A^TP_kB+N)(R+B^TP_kB)^(-1)(B^TP_KA+N^T)+Q
对于无限时间长度的离散时间线性系统(x_{k+1}=Ax_k+Bu_k),考虑性能指标:
J=\sum_{k=0}^{\infty}(x_k^TQx_k+u_k^TR_k+2x_k^TNu_k)
使性能指标最小的控制规律为u_k=-Kx_k
其中K=(R+B^TPB)^{-1}(B^TPA+N^T)
P是离散代数Riccati方程的唯一正定解
P=A^TPA-(A^TPB+N)(R+B^TPB)^{-1}(B^TPA+N^T)+Q
2 MPC
模型预测最早应用于过程控制中,在每个周期都使用模型迭代预测未来事件并进行处理。模型预测的性能指标与有限时间长度的离散时间线性系统相似:
J=\sum_{i=1}^N \omega_{x_i}(r_i-x_i)^2+\sum_{i=1}^N\omega _{u_i} \Delta u_i^2
通过性能指标,将控制问题转换为一个二次规划问题。获得模型后可以直接列写性能指标,然后交给QP解算器来处理。
3 对比
控制器结构:LQR控制器结构时固定的(u_k=Kx_k)。MPC没有固定的控制器结构,使用QP解算器求得是一个最优的控制轨迹。实施时每次执行最优轨迹中的一个控制器输出,下一个周期再根据新的状态重新求解,实施新的轨迹中的第一个控制器输出。
运行速度:通常使用的LQR控制器是基于无限时间长度设计的,可以先根据模型离线计算设计控制器。在实际运行时仅需要使用离线设计的控制器,在线运算量很小。MPC需要实时求解二次规划问题,运算时间远远大于LQR。这也是MPC广泛应用与过程控制中,而在动力学控制中应用有限的主要原因。
约束:受求解方法限制,LQR很难考虑系统输入与状态的约束。通常约束都是在控制器的输出侧增加饱和函数,而在设计控制器时并没有考虑。MPC可以在设计控制器时就把约束考虑在内,提高了模型精度。
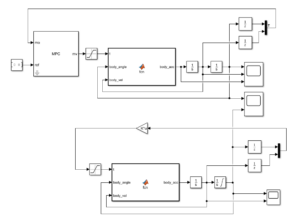
4 仿真
两个MATLAB function模块中包含的都是两轮车的非线性模型,
模型的输入是电机转矩,输出是车体角加速度。
function body_acc = fcn(t,body_angle,body_vel)
body_acc=(+1429.48*sin(body_angle)-1215.55*t-2083.85*t*cos(body_angle)-3.87597*sin(2*body_angle)*body_vel^2)/(2.91931+cos(body_angle)^2+8.75194*sin(body_angle)^2);\frac{1}{z}模块模拟的是采用过程。MPC、K*u两个模块是分别使用MPC和LQR两个算法根据两轮车线性化后的模型设计的控制器。