通常在描述物体旋转时,一般用其绕直角坐标系中哪个轴旋转多少度来描述。但是这种描述方式在特定情况下会发生死锁现象,导致两个旋转轴重合,丧失了对一个自由度的描述。在地面上这类问题出现较少,但是对飞行器等场所,这类问题是很严重的。本文将介绍 四元数基础概念 , 解决这类锁死的问题。
1 为什么需要用四元数
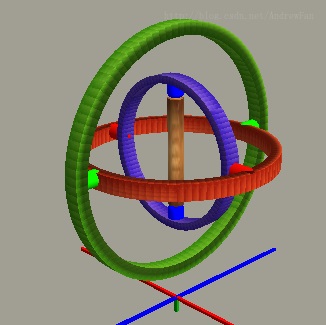
这里引用欧拉角与万向节死锁中的动画进行说明。我们要描述中间棕色圆柱的旋转,周围的绿色、红色、蓝色圆环分别代表x、y、z三个旋转轴。在此时,中间棕色圆柱无论如何旋转都可以分解到这三个旋转轴上。。
将蓝色圆环向任意方向旋转90°,如下图所示。此时蓝色圆环旋转轴和绿色圆环旋转轴重合,致使我们丧失了动画中旋转方向的描述。这个现象就是万向节死锁现象。
为了解决这个问题,出现了使用四元数描述物体旋转的方法。
2 四元数的定义及基本性质
四元数定义为
q ≡ a + b i + c j + d k(a, b, c, d∈ R )
四元数的定义与复数类似,但是他有三个不同的虚数单位。虚数单位之间相乘不满足交换律,结果如下。
| × | 1 | i | j | k |
| 1 | 1 | i | j | k |
| i | i | -1 | k | -j |
| j | j | -k | -1 | i |
| k | k | j | -i | -1 |
此外,我们还经常将四元数中的实部和虚部分开,用一个矢量表示其虚部,写成一个标量和矢量的有序对形式。
q ≡ [s, v](v = b i + c j + d k ; a, b, c, d∈ R )
3 用四元数表示3D旋转
一矢量v绕轴u旋转θ度后变为v’可以表示为四元数相乘的形式
v’ = qvq* = qvq-1 ( 其中v=[0,v], q=[ cos(θ/2), sin(θ/2)u] )
还可以表示为矩阵与矢量相乘的形式
\mathbf{v}'=\begin{bmatrix} 1-2c^2-2d^2 & 2bc-2ad & 2ac+2bd \\2bc+2ad & 1-2b^2-2d^2 & 2cd - 2ab \\2bd-2ac & 2ab+2cd & 1-2b^2-2c^2 \end{bmatrix}\mathbf{v}其中 a = cos(θ/2), b = sin(θ/2)ux, c = sin(θ/2)uy, d = sin(θ/2)uz。
4 四元数与欧拉角的转换
将欧拉角转换为四元数
\begin{aligned}\mathbf{q}&=\begin{bmatrix} cos(\psi/2)\\0\\0\\sin(\psi/2)\end{bmatrix}\begin{bmatrix} cos(\theta/2)\\0\\sin(\theta/2)\\0\end{bmatrix}\begin{bmatrix} cos(\phi/2)\\sin(\phi/2)\\0\\0\end{bmatrix}\\&= \begin{bmatrix} cos(\phi/2)cos(\theta/2)cos(\psi/2)+sin(\phi/2)sin(\theta/2)sin(\psi/2)\\sin(\phi/2)cos(\theta/2)cos(\psi/2)-cos(\phi/2)sin(\theta/2)sin(\psi/2)\\cos(\phi/2)sin(\theta/2)cos(\psi/2)+sin(\phi/2)cos(\theta/2)sin(\psi/2)\\cos(\phi/2)cos(\theta/2)sin(\psi/2)-sin(\phi/2)sin(\theta/2)cos(\psi/2)\end{bmatrix}\end{aligned}将四元数转换为欧拉角
\begin{bmatrix}\phi \\ \theta \\ \psi \end{bmatrix}=\begin{bmatrix}atan2(2(q_0q_1+q_2q_3),q-2(q_q^2+q_3^2))\\asin(2(q_0q_2-q_3q_1))\\atan2(2(q_0q_3+q_1q_2),1-2(q_2^2+q_3^2))\end{bmatrix}