本文将简洁地介绍Matlab system identification工具箱的使用方法,并使用该工具箱进行两轮车模型地辨识,对比分析不同辨识方法的实验结果。
一、系统辨识工具箱使用方法
数据导入:
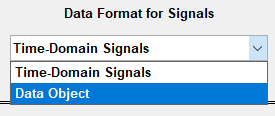
我现在使用的都是时域数据,所以点击左上角的导入数据,然后点击时域数据,出现如下窗口。分别填入相关变量名称和参数导入即可。
另一个方法是在matlab中先处理一下数据,建立一个data object,然后导入object即可。其他相关参数可以自动填写。使用iddata函数建立object,具体函数相关说明参见matlab手册。代码中input、output是提取出的系统的输入输出。swp是从实际系统中采集到的实验数据。data是建立的data object。
input=swp*[0; 0; 0; 1; 0; 0; 0]; output=swp*[0; 0; 0; 0; 0; 0; 1]; time=swp*[1; 0; 0; 0; 0; 0; 0]; data=iddata(output,input,0.002);
数据处理:
导入数据后不要直接进行拟合,最好先进行一些数据处理,尽可能的减少噪声对辨识的影响。
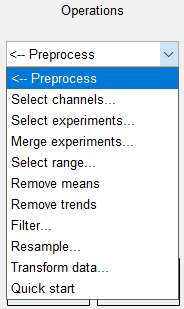
所有的信号都显示在左侧的data views中。先将需要处理的信号拖至working data中,然后选择需要进行的处理。我使用了remove means和filter两个处理方法。
拟合:
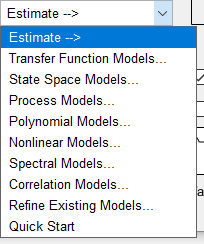
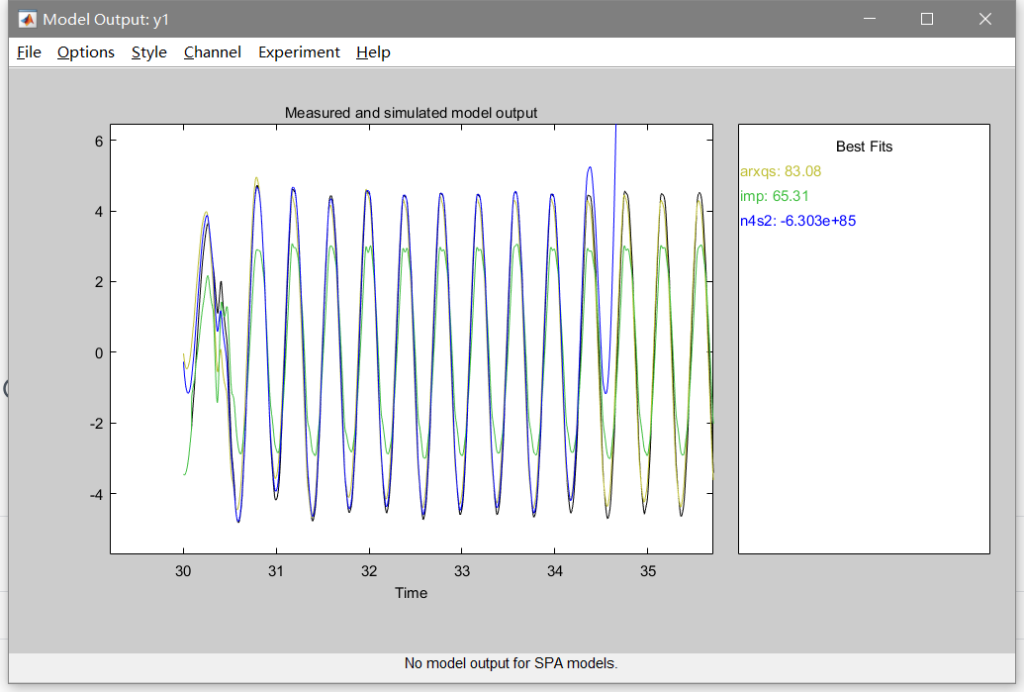
采集数据时最好采集两次,一次用于拟合,一次用于验证。在数据处理时对拟合所用的数据可以根据具体情况幅度较大地处理,而用于验证地数据尽可能少地处理。如果不方便实验或者已经采集完了数据,可以将一次数据裁开成两部分分别使用。可以选择模型进行一些设置后拟合,也可以使用quick start使用常用的几个模型进行拟合测试。下图分别是支持的模型和quick start的结果
二、两轮自平衡机器人模型
开始我一直希望使用理论模型推导,保留一些难测量的参数作为变量,然后进行参数辨识。两轮车的连续时间模型比较简单,设置状态为角度、角速度,输入量为电机加速度,其状态空间模型中A阵、B阵都仅含一个未知量。希望构建一个灰箱模型,辨识这两个参数。实验后出现的问题是实际工作的都是离散的环境不能直接使用连续时间系统模型进行辨识。如果强行转换为离散模型,则连续时间模型中的A、B阵的未知量会扩散影响到离散时间模型中A、B阵中每一个元素。这样使用灰箱模型与使用黑箱模型无异。
我犯的另一个错误是开始使用错了输入。受硬件条件限制,虽然计算模型时使用的输入量是加速度,但是我只能控制电机的速度和位置。为实现控制加速度的效果,我将控制器输出的加速度进行积分得到电机速度,再将电机速度发给电机驱动器。建模时,我认为积分为我设计的控制器环节中,不应该算在模型里,所以我使用的输入量时电机速度。这时候问题来了,为什么开始计算数学模型时使用的是加速度呢?因为电机加速度到车体角度的模型阶次最低,这样线性化后的模型准确度高。由此可见,拟合模型时也应该选用电机加速度作为模型输入。
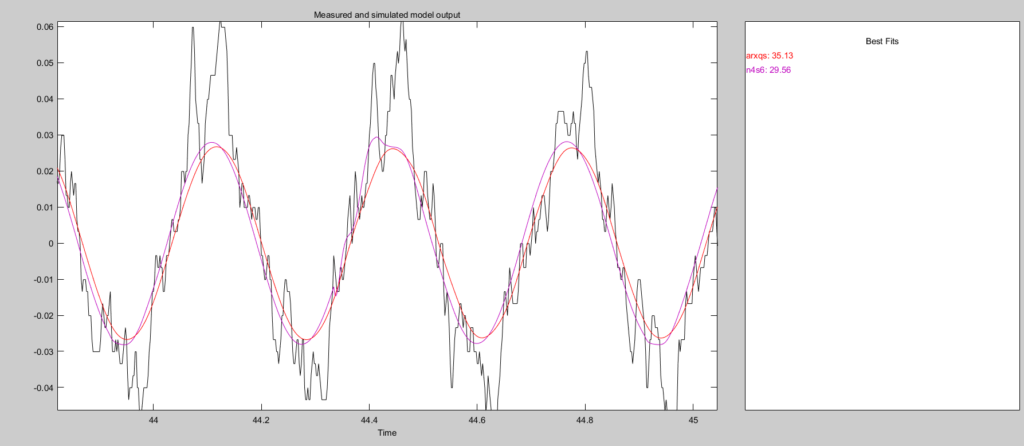
arxqs、imp、n4s2分别是离散ARX模型、脉冲响应模型、状态空间模型。虽然单从结果看状态空间模型的结果最不好,但两轮车本身就是一个不稳定模型,在测试模型时没有闭环,离散ARX模型和脉冲响应模型都能长时间保持稳定,所以我更倾向与先使用状态空间模型进行后面的测试。
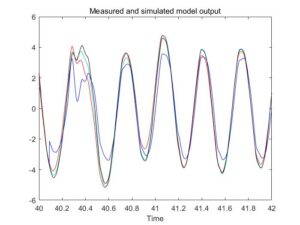
缩短测试数据的时间后得到在预测2s数据时,状态空间模型的效果最好。