上一篇文章中对两轮车的模型进行了验证。核心思想是用模型和输入估计系统的后面的输出,再根据实际采得的数据进行比较以对模型进行验证。这里模型的输出是两轮车的车体角度。实际工作中,该角度是通过加速度计和陀螺仪两个传感器的数据融合得到。整个系统工作结构如下图所示。这里 融合模型 较准确,以其输出作为标准,与两轮车模型的输出做比较。比较结果标志折两轮车模型的准确性。
本文目标是简化模型,直接使用电机加速度估计加速度计和陀螺仪数据,这样在实际使用中减少计算量,提高程序运行效率。
传感器数据融合模型
加速度计测量的是加速度,在忽略车体运动的加速度时,车体唯一的加速度是重力加速度。所以在低频区域,加速度计测量的数据可以转换为车体角度。陀螺仪测量的是车体角速度,可以通过积分得到车体角度。积分过程中,噪声会不断累积使结果产生漂移。所以陀螺仪的动态性能较好。这里各取所长,融合加速度计数据和陀螺仪数据估计真实的车体角度。
本文使用卡尔曼滤波器对车体角度进行估计。使用卡尔曼滤波需要给出系统模型、系统输入、输出以及输出和状态的方差。这里使用状态空间模型构建系统,输入输出分别是角速度和角度。设X为车体真实的角度。由机理得A=1 B=Ts C=1
\begin{gathered} X_{k+1}=A*X_k+u_k\\ Y_{k+1}=C*X_{k+1} \end{gathered}模型整合
整合的核心是在离散系统中对输出求导。两轮车模型输出是车体角度可以直接对应加速度计数据,另需要对车体角度求导得车体角速度对应陀螺仪数据。
\begin{aligned}Y'_{k+1}&=\frac{Y_{k+1}-Y_k}{T_s}=\frac{C*X_{k+1}-C*X_k}{T_s}\\ &=\frac{C*(A*X_k+B*u_k)-C*X_k}{T_s}\\ &=\frac{C*A-C}{T_s}X_k+\frac{B}{T_s}u_k \end{aligned}对应得到新的系数
\begin{matrix} A=A_{old}& B=B_{old}\\ C=\begin{bmatrix} C_{old}\\ \frac{C_{old}*A_{old}-C_{old}}{T_S} \end{bmatrix}& D=\begin{bmatrix}0\\ \frac{B}{T_S} \end{bmatrix} \end{matrix}仿真
仿真程序与上一篇得区别主要在于新的模型有两个输出,所以C是个矩阵而不是一个常数,此外新增了D矩阵。
for i=2:length(input)-steps %时间更新方程
x(:,i)=ax(:,i-1)+binput(i-1);
p=apa'+q; %模型预测误差统计
est_x=x(:,i);
for j=0:steps
est_output(:,i+1)=cest_x+dinput(i);
error_output(:,i)=error_output(:,i)+abs(output(i+1,:)'-est_output(:,i+1));
est_x=aest_x+binput(i+j);
end %状态更新方程
k=pc'(cpc'+r)^(-1);
x(:,i)=x(:,i)+k(output(i,:)'-(cx(:,i)+dinput(i-1)));
p=(eye(2)-kc)*p;
end完整程序:kalman_2var.m
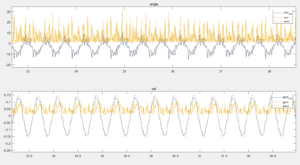
下图是5步预测的结果。效果没有上一篇文章中好,因为陀螺仪和加速度计都不能作为标准数据做校准使用。化简模型的主要意义在于简化后面运算量,而不在于检验模型正确性。