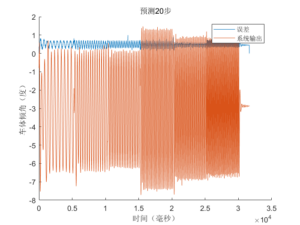
本文主要是对上一篇文章中通过matlab系统拟合工具箱得到的模型进行 两轮车模型验证 。首先使用卡尔曼滤波器进行状态估计,然后迭代模型根据输入预测未来控制对象输出。统计预测的输出和实际输出误差作为评价手段。比较误差与预测步数、系统输出之间关系,评价模型的可用性和最佳预测步数。
状态估计
使用matlab系统拟合工具箱中得到最佳模型是状态空间模型。使用状态空间模型出现的首要问题就是状态估计。之前我希望通过参数辨识的方法辨识出两轮车的状态空间模型,这样状态含有物理含义,可以直接使用传感器数据求解状态。但是现在得到的模型是通过黑箱模型辨识得到的,无法直接得到系统状态。
这里使用kalman滤波器估计状态。kalman滤波器以实现简单、效果显著的滤波效果为大家所知,但其本质是一个状态观测器。不断地在预测状态和根据实际数据校正状态中循环。姿态解算中,将实际姿态角设为状态,传感器数据作为系统输出,再估计状态。
滤波器核心以以下几个式子构成,其中a、b、c源自状态空间模型中的系数,x是状态,u是输入,q、r、p分别是过程激励噪声协方差矩阵、观测噪声协方差矩阵、估计误差协方差。
时间更新方程
x=a*x+b*u
p=a*p*a'+q
状态更新方程
k=p*c*(c*p*c'+r)^(-1)
x=x+K*(z-c*x)
p==(i-k*c)*p
matlab实现
部分代码:
%时间更新方程
x(:,i)=a*x(:,i-1)+b*input(i-1);
p=a*p*a'+q;
%模型预测误差统计
est_x=x(:,i);
for j=1:steps
est_output(i+j-1)=c*est_x;
error_output(j)=error_output(j)+abs(est_output(i+j-1)-output(i+j-1));
error_sum_output(i)=error_sum_output(i)+abs(est_output(i+j-1)-output(i+j-1));
est_x=a*est_x+b*input(i+j-1);
end
%状态更新方程
k=p*c'*(c*p*c'+r)^(-1);
x(:,i)=x(:,i)+k*(output(i)-c*x(:,i));
p=(eye(2)-k*c)*p;所有代码:kalman.m
实验结果
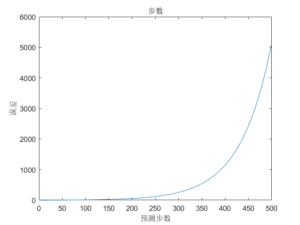
由第一张图可以看出预测超过200步(一步为一个采样周期:2ms),误差出现指数型增长。经过反复测试,在不考虑计算量的基础上预测20~50步为宜。